Welcome to a new post where, I have to admit, I’d forgotten what I’d written in a previous one!
In Mathematics Question – Number 15 and beyond! I’d said:
“From Mathematics Question – Number 17, onwards, I plan to post each question on the blog, as well, with extra comments that will then appear in the Mathematics Questions – Newsletters. So, basically, each question, plus comments, will become part of the blog and then the newsletter will appear periodically, bringing together, each time, three questions plus comments (as it does now). Hope that makes sense!”
The above didn’t materialise! Oops! What will happen is, I will be publishing the questions as normal on my website, nilsbirdtraining.com/mathematics-resources, and then the newsletter will be published in this blog.
So, here goes with Mathematics Questions – Newsletter No. 5.
Welcome to Mathematics Questions – Newsletter No. 5 – support for Mathematics Questions 17 to 19
Download Mathematics Questions – Newsletters 1 to 3 here. Click Mathematics Questions – Newsletter No. 4.
Before I dive into the newsletter, I thought I’d point out that you can’t receive the Mathematics Questions Newsletter directly anymore. You have to sign up for blog notifications instead. Sign up here.
To contact me regarding anything to do with this newsletter, use the contact details shown in the side bar.
Mathematics Question 17 – the skill of thinking, example 1
time (12 hour/24 hour clock, timetables), fractions – GRADES 5 through 8
Abdul lives in Gonnersburg. He travels, once a week, on the train to see his nephew, who lives in Carlson. The journey takes 57 minutes.
It takes Abdul 23 minutes to walk from his house to the train station and he always likes to arrive 10 minutes before a train is due to leave.
Train departures between Gonnersburg and Carlson are shown below:
| First train | Last train | |
| Gonnersburg to Carlson | 04:35 | 22:05 |
| Carlson to Gonnersburg | 04:55 | 22:25 |
Trains leave every 30 minutes in both directions.
On Thursday 14th August Abdul travelled to Carlson. He spent 4 hours 27 minutes with his nephew. He also spent ¾ of an hour shopping. He arrived home again at his house at 19:43.
a) What was the latest time Abdul could have left home to start his journey?
(Provide a complete, convincing argument to justify your answer.)
When Abdul was shopping, he bought a 3-DVD boxset of the documentary ‘Southern African Safari Adventures’. Each DVD contained 9 episodes. Each episode was 55 minutes long.
b) Abdul decided that he wanted to watch the complete boxset, in the evenings over several days, with his friend Mo. However, he only had time to watch the DVDs during the week, and he arrived home from work at 6:45 pm and went to sleep by 10:40 pm.
Suggest a suitable schedule that Abdul and Mo followed that allowed for breaks and time to discuss the episodes.
(Think about: what are the implications for watching a TV/DVD screen for too long? are there recommended time limits that it would be advisable to follow? how much time would a discussion take?)
Download Mathematics Question – Number 17 – without answers
Download Mathematics Question – Number 17 – with answers
This is the first question in my series on the skill of thinking. It is focused on Grades 5 to 8. Rather than having particularly difficult mathematics, the student is presented with the need to think through a detailed situation to arrive at an answer. (In Mathematics Question – Number 18 I started to write about the skill of thinking and how I’d write further posts about it. Well, they are to come!)
You will see that the information given to the student is quite complex. Before even thinking through what methods they need to answer parts a) and b), the student needs to understand: the train journey time; the time it takes to walk to the station; the fact that Abdul likes to arrive a station early; a train timetable; the times involved (including fractions) when Abdul travels to see his nephew.
When the student looks at part a), they are presented with a bit of a challenge! They need to find out the latest time that Abdul could have left home on the day that he went to see his nephew. Now, you might ask: “Why this is a challenge?” Well, I believe it is because the student now has to work with all the information, seeing how to integrate it, all within the idea of working backwards from the home arrival time.
So, this idea of working backwards in mathematics can be, I think, a hard thing for students to get their head round! My classic example I provide for students is: “This is the answer, what is the question?” A simple example I have used in tutoring this year (as a starter to gauge what level of mathematics a student might have) is: “12 is the answer, what is the question?” Now, I think a grade 5 to 8 student would immediately give, say, 6 + 6, unless you directed them to think of something more tricky, like 5/6 + 67/6, or didn’t allow +, -, x or / to be used. So, they might give an equation where 12 is the solution, or provide some data where 12 is the median. In the AQA 90 problem booklet, the task Javelin B is a good example of a question that can be solved by working backwards. (I highly recommend the AQA 90 problem booklet as a source of material for your students. Lots of good advice, as well as the problems.)
Returning to part a), as the student works backwards through the problem, they will come across some interesting ‘extras’ that might trip them up. For example, there are extra bits of time that slip in because the Abdul’s journey does not immediately involve going from one thing to the next!
I have provided an answer (for the way the problem can be interpreted, as far as I am concerned) but your students might find another. Whatever they do, they are told to: “Provide a complete, convincing argument to justify your answer.” Now, you, yourself, will have to make a judgement as to what the word complete means for your students.
Before part b), you can see I have added some additional information about the what Abdul bought whilst he was in Carlson – 3-DVD boxset of the documentary ‘Southern African Safari Adventures’. Each DVD contained 9 episodes. Each episode was 55 minutes long. Part b) then asks students to work out a schedule that Abdul, and his friend Mo, can follow to be able to watch the episodes (within some parameters).
With part b) there isn’t the same level of challenge for the student, as there is for part a), but there is more opportunity for a student to provide their own, reasonable solution.
You might ask: “What thinking is involved with part b)?” Well, I think: the student has to think carefully about how many episodes can be watched each night; they need to consider what is a reasonable amount of time to discuss an episode; how long should they break for. (As can be seen, I have provided prompts to get the student to think about such things)
So, how might we present this question in the classroom? Well, I think all the questions in this mini series fit very well into TPS – think, pair, share. Getting the students to think on their own (for, say, 1 minute), then sharing their thoughts in pairs (for another, say, 2 minutes) and finally sharing in larger groups/the whole class. An example of this method can be seen here:
TPS could be used, for example, at the very start, when you introduce the question – getting the students to read through the question on their own, then 1 minute of silent thinking/writing thoughts down about what they think the problem is asking them to do; then sharing these thoughts with a partner; then sharing in a wider group/whole class.
As you support students’ understanding of the problem, you might suggest questions they might ask themselves: what does it mean to arrive 10 mins before a train is due to leave? how will this affect Abdul’s journey? what times do trains arrive and leave at both stations? what happens is Abdul misses a train? will Abdul and Mo be able to watch more than one episode per night?
This question poses challenge for some students (and, no doubt, adults as well!). What about the next one?
Mathematics Question 18 – the skill of thinking, example 2
money, percentages including percentage discount – GRADES 5 through 8.
The table shows information about two books:
| Published | Retail Price | |
| Fishing For Beginners | September 2021 | $23.00 |
| 20 Songs For Every Occasion | December 2019 | $17.50 |
The two books can be purchased at Azop.com, an online store, or Reading For Pleasure, a bookstore found at Main Square, Tannersville.
Both of the stores have their own membership schemes to entice people to become regular customers.
The table shows information about the membership schemes:
| Membership Cost | Benefit | New Member Offer | |
| Azop.com | $2.50 per month | 1 point = 3.5 cents $3.50 fixed postage charge on all purchases | 1 month free plus 5% discount off the first purchase |
| Reading For Pleasure | $4.50 per month | 1 point = 0.7% | 1 month free plus $2.00 discount off the first purchase |
Customers collect points based on the number of purchases they have made. These points can then be used to obtain discounts off future purchases.
Ashrif and Sidra are friends, who both live in Tannersville. Ashrif is a keen fisherman and Sidra loves singing. Ashrif is a member of the Reading For Pleasure scheme. He has collected 15 points. Sidra is a member of the Azop.com scheme. She has collected 150 points.
a) Decide which store is the cheapest way for Ashrif and Sidra to purchase the two books.
(Provide a complete, convincing argument to justify your answer.)
b) Find the percentage saving that Ashrif and Sidra make when they purchase their books at the cheaper store.
c) Suggest other suitable benefits that the membership schemes could provide for regular customers.
Download Mathematics Question – Number 18 – without answers
Download Mathematics Question – Number 18 – with answers
This is the second question in my series on the skill of thinking. Again, focused on Grades 5 to 8. It is different to Mathematics Question – Number 17. There is less information overall, but two different tables to interpret.
The question was influenced by online companies who have similar membership schemes. I am wanting the student to compare the two companies, and make some judgements based on what they know about Ashrif and Sidra.
So, one of the first things the student has to do is make sure they understand the two tables, especially the membership structures. A question they might ask themselves is: “Is all the information relevant?” Trying to decide this is a skill in itself, I think. How many times do we have to decipher paragraphs of information/tables of data in life?
A quick search on the internet will bring up those who talk about the skills needed for working with information, for example:
Thinking, again, about the membership schemes, the need to interpret this sentence is crucial: “Customers collect points based on the number of purchases they have made. These points can then be used to obtain discounts off future purchases.” How to apply the discounts clearly needs to be understood!
So, with part a), the student has to work with all the relevant information to find the cheapest way of buying the books. Is it relevant who buys which book, they might ask? Well, even if it isn’t, it would make sense that Ashrif and Sidra buy the book they are most interested in!
With part b), there is just the need to do the calculation. No research needed! However, if figures are wrong in part a), then part b) will be wrong. So, what do we do, as teachers, in this circumstance? In an examination context, we use the concept of follow through (ft) which, no doubt, a number of you are familiar with. (I talk about mark schemes, specifically, in Mathematics Questions – Newsletter 3 and 4) The idea with ft is that the student is not penalised for when some numbers are wrong but are inputted correctly in a formula. As in:
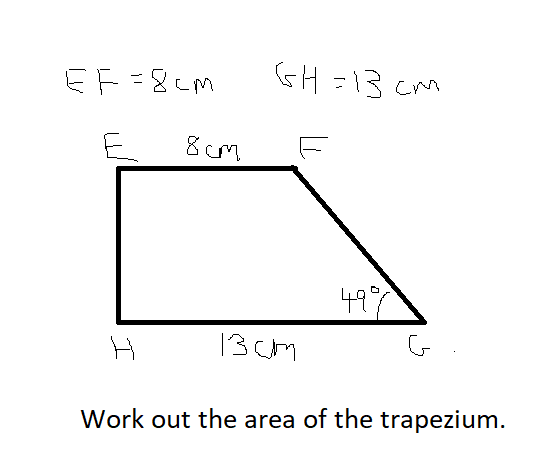
The mark scheme for this question might be something like:
- M1 – tan 49 = h / 5, where h stands for the height of the trapezium
- M1 – h = 5 x tan 49
- M1 ft – 1/2 x (13 + 8) x their h
- A1 – 60.39 to 2 decimal places
So, you can see that the student could get up to three marks if they get the value of h wrong but input it correctly in the trapezium formula. (I know there are equivalent methods within the question but, I think, you get the point!)
So, for part b), if your students have a different answer to mine, you might still be able to award them some credit.
With part c), there is a completely open opportunity for a research project on membership schemes. So, an opportunity for cross-curricula activity!
As with Mathematics Question 17, TPS is an ideal method for introducing this question in the classroom, along with providing suitable questions they might ask themselves: what information can I throw away? should Ashrif and/or Sidra join the other membership programme? which store is my 100% when I am finding the percentage discount?
Finally, we turn to Mathematics Question 19.
Mathematics Question 19 – the skill of thinking, example 3
money, time, percentages including percentage discount – GRADES 5 through 8
Kingswood Bowling Alley has the following opening times for ten-pin bowling:
| Mon to Fri | Sat/Sun | |
| October to March | 09:00 – 20:00 | 08:00 – 23:00 |
| April to September | 08:00 – 22:00 | 07:00 – 01:00 |
The prices for bowling are as follows:
| 12 years old and under | Over 12 years old | Special offer | |
| By the game | $7.69 | $9.49 | N/A |
| Daytime by the hour – until 17:00 | $14.89 for 2 hours | $17.79 for 2 hours | N/A |
| Late Night Pass – 22:00 until closing time | $18.69 per person | Unlimited bowling |
Groups of four, or more, have a 10% discount on their first game. If two, or more, games are booked, a 15% discount is provided.
Pierre, Sidra, Mo and Nat are four friends (all adults), who are planning to go bowling, together, on a regular basis; around once, or twice, a month. They are thinking about varying their playing times between the daytime and the evening.
a) Plan a suitable schedule that the four friends could follow, over a period of six months, between February and July. Think about what prices they will pay.
b) Modify your plan, planning some dates to cover occasions when:
- not all of the friends can bowl together
- the friends only have one hour to spare to go bowling
- younger family members (less than 12 years old) are also included
c) Investigate the scoring of ten-pin bowling. Plan a suitable two-game scenario, showing what scores the four friends achieved for both games.
Download Mathematics Question – Number 19 – without answers**
** there is no answer version as the answers from students will vary.
This is the third question in my series on the skill of thinking. Again, focused on Grades 5 to 8. It is the most flexible of the three questions, as there is a lot more opportunity for the student to create their own answers.
As with Mathematics Question – Number 18, the student has to comprehend tables of information. I am wanting the student to make judgements and create plans, based on the given information.
The question’s flexibility reminds me of the previous GCSE maths exams we used to run in the UK where they had a coursework element. For example, these materials were produced in support of the examination:
https://www.mathshell.com/materials.php?series=gcse
As with Mathematics Question – Number 18, one of the first things the student has to do is make sure they understand the two tables, as well as any available discounts. I don’t think we can say there is irrelevant information, as the student might make use of any of it throughout the question.
With parts a) and b), the student needs to plan carefully, bearing in mind the any conditions I am placing on the plan; part c) allows the student to find out all about the scoring system used in ten-pin bowling, and create some game scenarios. So, all parts research galore!
For part c), I think these websites would be worth a look:
https://www.topendsports.com/sport/tenpin/index.htm
https://www.bowl.com/Welcome/Welcome_Home/Keeping_Score/
As with Mathematics Questions 17 and 18, TPS is an ideal method for introducing this question in the classroom, along with providing suitable questions they might ask themselves: is all the information relevant? how will any discounts work? are there any suitable diagrams I could draw/use to explain how the scoring works?
Well, that’s the end of, what I think, is quite a long Mathematics Newsletter. I hope you enjoyed it!
Please, connect with me over anything found in this Mathematics Newsletter, or anything else of interest!
Best wishes for the moment.
See you next time.
David
nilsbird training
